※ 本ホームページは Internet Explore を推奨しており、バージョン6.0以降で快適にご覧いただけます。
	電力・エネルギーシステム分野における最適化問題の解法に関する研究 ※各図表をクリックしますと拡大表示されます。ウインドウを最大化してご覧下さい。 ●研究の背景 　現代社会では様々な分野で最適型のモデルを使った分析が用いられています。例えば、近年環境問題に対する意識が高まっており、エネルギー消費量や二酸化炭素排出量を削減するエネルギーシステムの分析などに最適化モデルが用いられています。また、近年の電力事業の規制緩和により、電力系統において従来とは異なった系統状態が発生すると考えられ、そのような場面でも最適化モデルを利用した分析が行われています。このようなモデルでは対象をするシステムの複雑化により最適化に費やされる計算時間が膨大に増加したり不安定になったりします。そのためより速く安定的な解法が望まれています。　 ●研究の概要 　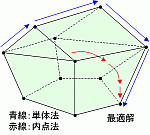最適化問題の解法として古くからある単体法は実行可能領域の1つの端点を初期点とし、隣接する端点を辿って最適解に到達する手法です。それに対して、1980年代に登場した内点法は実行可能領域の内部に初期点をとり、内部を通って最適解に到達する手法で大規模な問題に対して有効です。 　エネルギーシステムの最適計画・運用問題は、発電機などの各機器の台数や運転状態などを最適化する0-1混合整数計画問題として定式化されます。また、電力系統の最適化問題の一つである最適潮流計算は発電電力コストなどを最小化する潮流状態を決定する非線形計画問題として定式化されます。 　このようなエネルギーシステムや電力系統の最適化問題を解く際に、内点法の利用や問題の特徴を利用した手法の利用などによって計算時間の短縮や高いロバスト性を持つアルゴリズムに関する研究を行っています。 ●主な研究成果 　0-1混合整数計画問題に分枝限定法を適用する場合に、最初の緩和問題に内点法を用いた手法を提案し、大きな時間短縮を実現しました。また、部分構造反復法や分枝カット法を用いた計算時間の短縮も行ってきました。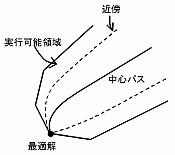 電力系統に関する研究では、PQ分離法を適用した高速な最適潮流計算の手法や直列制御機器を考慮した最適潮流計算の内点法による解法を提案しました。また、強い非線形性を有する最適化問題に対し、中心パスの近傍を利用した手法を提案し高いロバスト性を実現しました。 ●主要論文 1) 佐伯 修，境 政志，辻 毅一郎：デカップル版最適潮流計算における内点法の適用，電気学会論文誌B，Vol.119，No.6，pp.673-680，1999. 2) 沢井 一智，佐伯 修，辻 毅一郎：ある種の混合整数計画問題への内点法の応用，システム制御情報学会論文誌，Vol.14，No.2，pp.71-77，2001. 3) 長澤 和巳，佐伯 修，辻 毅一郎:最適潮流計算における中心パス追跡法の近傍定義に関する検討，電気学会電力・エネルギー部門大会論文集，No.19，pp.1-2，2005． << 研究内容のインデックスへ戻る